Predicting Power System Dynamics and Transients: A Frequency Domain Approach

The dynamics of power grids are governed by a large number of nonlinear ordinary differential equations (ODEs). To safely operate the system, operators need to check that the states described by this set of ODEs stay within prescribed limits after various faults. Limited by the size and stiffness of the ODEs, current numerical integration techniques are often too slow to be useful in real-time or large-scale resource allocation problems. In addition, detailed system parameters are often not exactly known. Machine learning approaches have been proposed to reduce the computational efforts, but existing methods generally suffer from overfitting and failures to predict unstable behaviors.

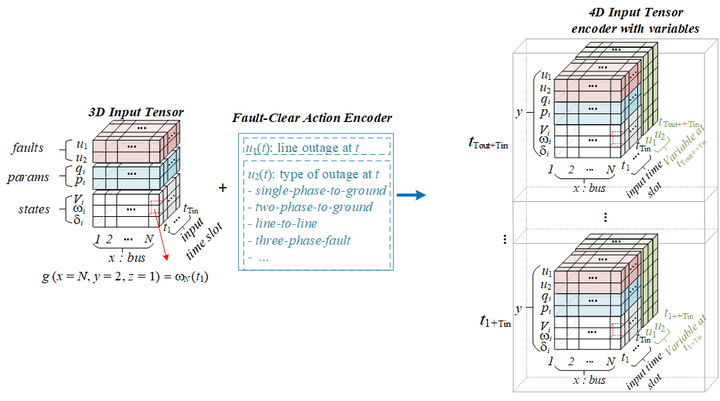
This paper proposes a novel framework for power system dynamic predictions by learning in the frequency domain. The intuition is that although the system behavior is complex in the time domain, there are relatively few dominate modes in the frequency domain. Therefore, we learn to predict by constructing neural networks with Fourier transform and filtering layers. System topology and fault information are encoded by taking a multi-dimensional Fourier transform, allowing us to leverage the fact that the trajectories are sparse both in time and spatial (across different buses) frequencies. We show that the proposed approach does not need detailed system parameters, speeds up prediction computations by orders of magnitude and is highly accurate for different fault types.