Reinforcement Learning for Optimal Frequency Control - A Lyapunov Approach

The increase in penetration of inverter-based resources provides us with more flexibility in frequency regulation compared to conventional linear droop controllers. Using their power electronic interfaces, inverter-based resources can realize almost arbitrary responses to frequency changes. Reinforcement learning (RL) has emerged as a popular method to design these nonlinear controllers to optimize a host of objective functions.

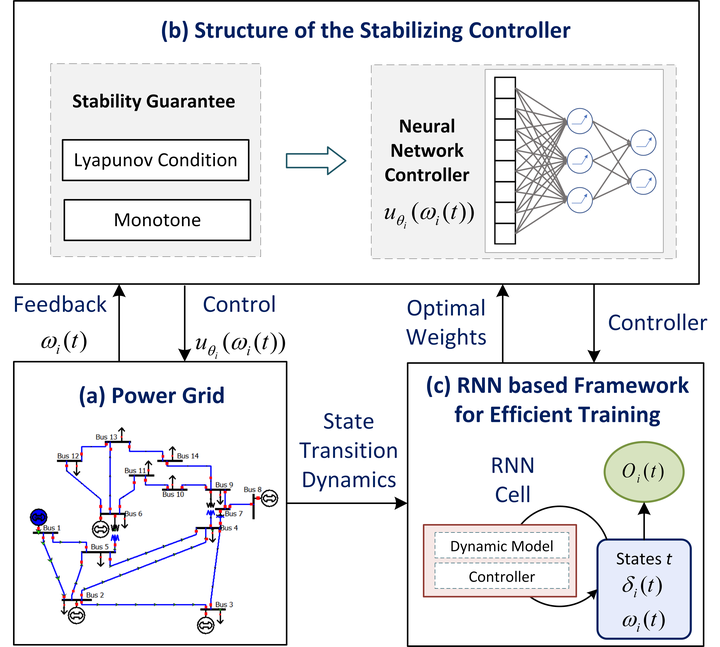
The key challenge with RL-based approaches is how to enforce the constraint that the learned controller should be stabilizing. In addition, training these controllers is nontrivial because of the time-coupled dynamics of power systems. In this paper, we propose to explicitly engineer the structure of neural network-based controllers such that they guarantee system stability by design. This is done by constraining the network structures using a well-known Lyapunov function. A recurrent RL architecture is used to efficiently train the controllers. The resulting controllers only use local information and outperform linear droop as well as controllers trained using existing state-of-the-art learning approaches.