 Image credit: Unsplash
Image credit: Unsplash
Abstract
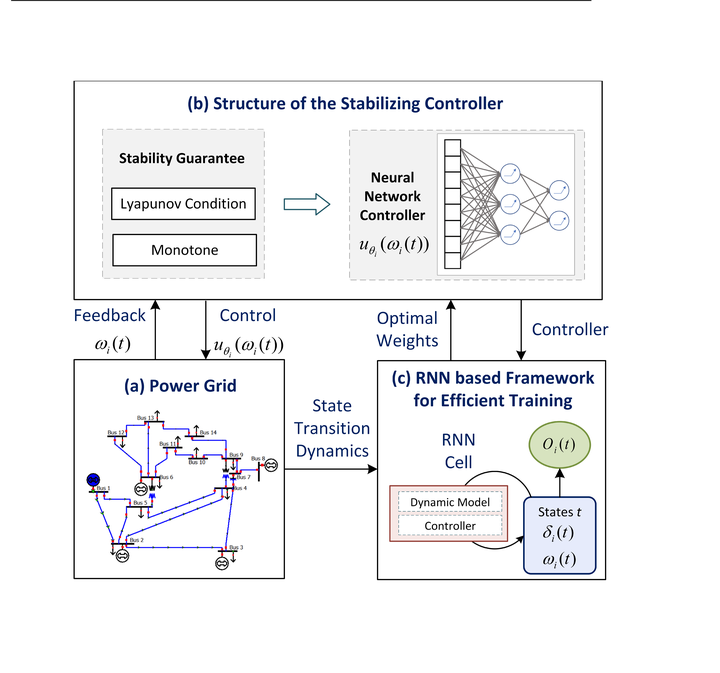
The increase in penetration of inverter-based resources provide us with more flexibility in frequency regulation of power systems in addition to conventional linear droop controllers. Because of the fast power electronic interfaces, inverter-based resources can be used to realize complex control functions and potentially offer large gains in performance compared to linear controllers. Reinforcement learning has emerged as popular method to find these nonlinear controllers by parameterizing them as neural networks.
The key challenge with the learning-based approach is that stability constraints are difficult to enforce on the learned controllers. In addition, optimizing the controllers are nontrivial because of the time-coupled dynamics of power systems. In this paper, we propose to explicitly engineer the structure of neural network based controllers such that they guarantee system stability for all topologies and parameters. This is done by using a Lyapunov function to guide their structures. A recurrent neural network based reinforcement learning architecture is used to efficiently train the weights of controllers. The resulting controllers only use local information and outperform linear droop as well as strategies learned purely by using reinforcement learning.